Aufgabenbeispiele von 2. Strahlensatz
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
2. Strahlensatz (gleiche Seite)
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 16 | ||
| = |
2. Strahlensatz (2 Seiten)
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 4 | ||
| = |
2. Strahlensatz (3 Segmente)- schwer
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x und y.
Wir betrachten zuerst den Teil rechts vom Zentrum.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |||
| = | |⋅ 10 | ||
| = | |||
| = | | | ||
| = |
Nun betrachten wir den Teil links vom Zentrum.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 14 | ||
| = |
2. Strahlensatz (3 Segmente)- schwer
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x und y.
Wir betrachten zuerst den Teil rechts vom Zentrum.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 16.5 | ||
| = |
Nun betrachten wir den Teil links vom Zentrum.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 6 | ||
| = |
doppelter Strahlensatz (klein)
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x und y.
Nach dem 1. Strahlensatz gilt:
=
D=R\{
| = | |||
| = |
Wir multiplizieren den Nenner weg!
| = | |⋅( ) | ||
| = | |||
| = |
| = | |⋅ 2 | ||
| = | |||
| = | | | ||
| = | |:() | ||
| = |
(Alle Lösungen sind auch in der Definitionsmenge).
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |||
| = | |⋅ 11 | ||
| = | = 27.5 |
doppelter Strahlensatz (klein 2)
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x und y.
Nach dem 1. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 19.2 | ||
| = |
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 14.4 | ||
| = |
Strahlensätze (4 Var.) - schwer
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x, y, z und t.
Wir betrachten zuerst den Teil mit x.
Nach dem 1. Strahlensatz gilt:
=
| = | |||
| = | |||
| = | |⋅ 10 | ||
| = | |||
| = | | | ||
| = | = 17.5 |
Nun betrachten wir den Teil mit y.
Nach dem 1. Strahlensatz gilt:
=
D=R\{
| = | |||
| = |
Wir multiplizieren den Nenner weg!
| = | |⋅( ) | ||
| = | |||
| = |
| = | |⋅ 4 | ||
| = | |||
| = | | | ||
| = | |:() | ||
| = |
(Alle Lösungen sind auch in der Definitionsmenge).
Nun betrachten wir den Teil mit z.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |||
| = | |⋅ 4 | ||
| = |
Nun betrachten wir den Teil mit t.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 14.575 | ||
| = |
Strahlensätze (4 Var.) II - schwer
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x, y, z und t.
Wir betrachten zuerst den Teil mit x.
Nach dem 1. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 8 | ||
| = |
Nun betrachten wir den Teil mit y.
Nach dem 1. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 9 | ||
| = |
Nun betrachten wir den Teil mit z.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 6 | ||
| = |
Nun betrachten wir den Teil mit t.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 2.8 | ||
| = |
Strahlensätze (4 Var.) II - schwer
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x, y, z und t.
Wir betrachten zuerst den Teil mit x.
Nach dem 1. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 9 | ||
| = | = 15.75 |
Nun betrachten wir den Teil mit y.
Nach dem 1. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 22.75 | ||
| = |
Nun betrachten wir den Teil mit z.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 5.25 | ||
| = |
Nun betrachten wir den Teil mit t.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 10.5 | ||
| = |
Strahlensatz Anwendungen (schwer)
Beispiel:
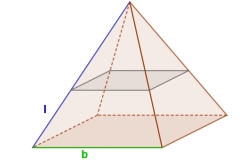
Die Grundfläche einer senkrechten quadratischen Pyramide ist b=36 m lang. Die Länge der Seitenkanten ist l=31,5 m. Die Pyramide wird parallel zur Grundfläche abgetragen, so dass ein Pyramidenstumpf entsteht. Die Länge der Seitenkanten l verkürzt sich dadurch von 31,5 auf 17,5 m. Wie breit ist dann die quadratische Fläche der Oberseite des entstehenden Pyramidenstumpfs?
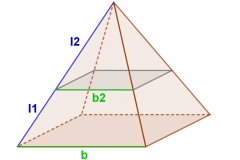
Wenn man in die Skizze ein paar Strecken einzeichnet, erkennt man eine Strahlensatzfigur:
Dabei gilt nach dem 2. Strahlensatz:
= bzw. =
Aus dem Text können wir herauslesen:
l = l2 + l1 =31.5
l1 = 17.5
l2 = 14
b = 36
Gesucht ist die Breite der neuen Oberseite. Wir wählen also b2 als x.
Jetzt können wir die Werte in die obige Strahlensatzgleichung einsetzen und erhalten:
=
| = | |||
| = | |⋅ 36 | ||
| = | = 16 |
b2 ist also .
Die Lösung ist somit: 16
