Aufgabenbeispiele von proportionale Zuordnung
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
Zweisatz
Beispiel:
Herr Tobrak hat einen neuen Handyvertrag abgeschlossen. Für eine Minute telefonieren bezahlt er nun 3 ct.
Wie viel kosten ihn 4 min telefonieren?
Zuerst stellen wir den Sachverhalt in einer Tabelle dar:
|
Um von 1 Minuten telefonieren in der ersten Zeile auf 4 Minuten telefonieren in der zweiten Zeile zu kommen, müssen wir mit 4 multiplizieren. Somit müssen wir auch die 3 ct mit 4 multiplizieren, um auf den Wert zu kommen, der den 4 Minuten telefonieren entspricht:
|
⋅ 4
|
 |
|
 |
⋅ 4
|
|
⋅ 4
|
 |
|
 |
⋅ 4
|
Damit haben wir nun den gesuchten Wert, der den 4 Minuten telefonieren entspricht: 12 ct
Zweisatz rückwärts
Beispiel:
Der Hersteller eines Powerdrinks wirbt damit, das 2100 g Protein in dessen 7kg-Großpackung drin sind.
Wie viel g Protein ist in 1 kg Powerdrink?
Zuerst stellen wir den Sachverhalt in einer Tabelle dar:
|
Um von 7 kg Powerdrink in der ersten Zeile auf 1 kg Powerdrink in der zweiten Zeile zu kommen, müssen wir durch 7 teilen. Somit müssen wir auch die 2100 g Protein durch 7 teilen, um auf den Wert zu kommen, der den 1 kg Powerdrink entspricht:
|
: 7
|
 |
|
 |
: 7
|
|
: 7
|
 |
|
 |
: 7
|
Damit haben wir nun den gesuchten Wert, der den 1 kg Powerdrink entspricht: 300 g Protein
Proportionalität überprüfen
Beispiel:
Prüfe, ob es sich um einen proportionalen Zusammenhang handelt; falls nicht, korrigiere die Werte.
Wir überprüfen zuerst, ob die 30 ct den 12 Minuten telefonieren entsprechen.
|
: 2
⋅ 3
|
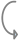 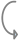 |
|
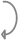 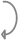 |
: 2
⋅ 3
|
Der Wert 30 ct war also falsch, richtig wäre 36 ct gewesen.
Jetzt überprüfen wir, ob die 30 ct den 10 Minuten telefonieren entsprechen.
|
: 4
⋅ 5
|
  |
|
  |
: 4
⋅ 5
|
Der Wert 30 ct war also korrekt.
