Aufgabenbeispiele von Anwendungen
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
Sinus und Thaleskreis (leicht)
Beispiel:
Das große Dreieck ist gleichschenklig.
Der blaue Halbkreis hat einen Durchmesser von u = 7 cm.
Die Länge der gemeinsamen Kante der beiden Dreiecke beträgt v = 5.9 cm.
Bestimme die fehlende Winkelweite α.
Am blauen Thaleskreis erkennt man sofort, dass γ ein rechter Winkel sein muss.
Nach der Definition des Sinus gilt im rechtwinkligen Dreieck sin(β)=
Damit folgt sin(β)==0.843 und somit β=57.4°
Wegen der Winkelsumme im Dreieck muss gelten: 90° + β + α = 180°.
Somit gilt α = 90° - β° = 32.6°.
Sinus und Thaleskreis (schwer)
Beispiel:
Das große Dreieck ist gleichschenklig. Bestimme die Länge der Strecke PQ.
Am blauen Thaleskreis über dem ersten Dreieck erkennt man sofort, dass γ ein rechter Winkel sein muss.
Als Nebenwinkel von γ muss natürluch auch δ ein recher Winkel sein.
Aufgrund der Winkelsumme im zweiten Dreieck folgt δ + ε + 34° = 180°.
Daraus folgt ε = 180° - 90° - 34° = 56°.
Mit Hilfe der Gleichschenkligkeit des großen Dreiecks kann mann nun β bestimmen: Es gilt ε + 2⋅β = 180°. Daraus folgt β = = = 62°
Mit Hilfe des Sinus kann man nun die Länge der gemeinsamen Seite g der beiden Dreiecke berechnen:
Da g die Gegenkathete von β ist, gilt: sin(β)=sin(62°) =
Damit folgt g = sin(62°) ⋅ 6cm ≈ 5.3cm
Nun können wir im zweiten Dreieck den Sinus anwenden und so die gesuchte Seite PQ herausfinden: sin(ε)=
Setzt man die bekannten Werte ein, so folgt sin(56°)=
Damit folgt: PQ = = 6.4cm
Trigonometrie Anwendungen
Beispiel:

Von einem Fenster in 13m Höhe kann man den entfernten Rand eines Kanals unter dem Winkel α=70° gegenüber der Senkrechten betrachten. Der vordere Rand des Kanals erscheinet unter dem Winkel β=25° gegenüber der Senkrechten. Wie breit ist der Kanal?
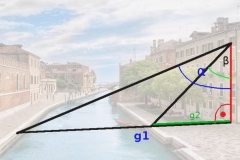
In beiden Dreiecken gilt für den Tangens: tan(α)=.
Da nach der Gegenkathete gesucht wird, stellen wir um zu
Gegenkathete g1=Ankathete ⋅ tan(α)=13 ⋅ tan(70°)
≈35.7172
Genau gleich verfahren wir mit dem anderen Dreieck:
Gegenkathete g2=Ankathete ⋅ tan(β)=13 ⋅ tan(25°)
≈6.062
Die gesuchte Strecke ist nun gerade die Differenz der beiden Gegenkatheten:
s=35.717 - 6.062 ≈ 29.655 m.
Winkel zw. Punkten im Koordinatensystem
Beispiel:
Berechne alle Längen und Winkel im Dreick ABC mit A(1|1), B(5|1) und C(5|4).
Runde die Ergebnisse auf eine Nachkommastelle.
Wenn man die drei Punkte in ein Koordinatensystem einträgt, erkennt man sofort, dass (zwischen B und C) a = 3 und (zwischen A und B) c = 4 sein müssen. Weil das Dreieck rechtwinklig ist, kann man b (zwischen A und C), also die Hypotenuse, mit dem Satz des Pythagoras berechnen:
Dreiecks mit Hilfe des Satzes des Pythagoras berechnen.b2 = 32 + 42
b2 = 9 + 16
b2 = 25
b = ≈ 5
Da a (zwischen B und C) und c (zwischen A und B) parallel zu den Koordinatenachsen sind, muss der Winkel in B β = 90° sein.
Den Winkel α können wir mit dem Tangens berechnen:
tan(α) = = = 0.75
Daraus folgt: α = arctan(0.75) ≈ 36.9°.
Wegen der Winkelsumme von 180° im Dreieck folgt: γ = 90°-36.9° = 53.1°
